Basic Biophysics for Biology
The subject of this discussion is taken from the title of a book written by Edgar K. Yeargers PhD, a professor of biophysics at Georgia Tech. His book was written so that student of physics would be able to understand that the rules of physics for nonliving systems also apply to living systems.
Our discussion will involve understanding the interaction of electric charges. By convention a proton is assigned to be a positive charge and an electron is assigned be a negative charge.
Material substances are mostly neutral in charge but are composed of large fixed positive and negative charges. If there is an imbalance in the charges, the material it is said to be “charged” with each charge exerting a force on the other- “unlike charges attract, like charges repel”.
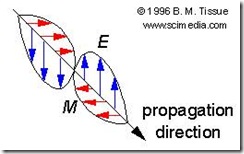
On the other hand, charges that are opposite in sign and equal in magnitude, when aligned along a common axis, are called an electric dipole. When dipole charges move, they move independently of each other. When oscillating up or down along their axis, they pass each other going in opposite directions. In doing so, a variable electric force and a corresponding electric field effect develops. The field effect can be propagated some distance away from the oscillating dipole and can be detected on the skin by an electromagnetic sensor.
In the laboratory dipole antennas generate large (macroscopic) radiations
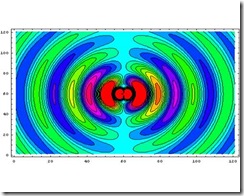
Below is an oscillating electrical dipole:
Source: http://en.wikipedia.org/wiki/Dipole
On a submicroscopic scale, as in living systems, the antenna is replaced by an oscillating emission source that cannot be measured directly. There is evidence that dipole generated radiations do exist and that they come from nuclei, electrons, light and chemical bonds and numerous other sources. It is postulated that oscillations in living systems produce propagated electromagnetic waves.
Electromagnetic radiations (waves) have:
Amplitude (height of the wave)
Amplitude is proportional to strength of the electric force
Amplitude may be positive or negative coinciding with the direction of the electrical charge resulting from the dipole movement
Frequency (rate of change of a charge in oscillating from positive to negative
Energy
Is proportional to the wavelength of the oscillating wave
Short wavelengths have higher energy than long wavelengths
Electric field effect
May be local, at the site of the oscillating dipole
May be propagated at a distant site such as, the skin or a secondary detection site
Propagation of the electric field is at the speed of light
Remember that a wave is a variable electric charge. It is not a line on a piece of paper that is represented as a sine wave.
Characteristics of electromagnetic waves
Interference
One of the characteristics of propagating waves is that they interfere with one another.
When the peaks and troughs of two identical waves meet, they are said to have a condition of constructive interference because the arithmetic sum of the resulting wave is bigger (more intense) than either of the two contributing waves.
When the peak of one wave coincides with the trough of another identical wave the arithmetic sum of the resulting wave is zero. This is a condition of destructive interference.
By using the electromagnetic model in the study of biology we use a paradigm built upon the most essential elements in our physical existence:
1. Oscillating dipoles producing variable electric fields
2. Variable electric fields propagating at a distance from the dipole source.
These two elements are found at all levels of structure.
They are found in:
Subatomic particles
Atoms
Molecules
Hydrated molecules essential in biology such as sols and gels
Cells
Tissue
Organs
Systems
Each level of structure has dipole depicted waves that are derived from components that make up structure, the result of constructive and destructive interference. For example, waves from subatomic particles are the components that make up an atom. Waves from atoms are the components of molecules, etc.
Locally, at the site where the variable electric field originates, a charge has its own amplitude, frequency and energy, that is, bits of information that gives the charge an identity. In that sense this model can be understood as being information technology. When applied to a living system it is information technology in biology.
Electric fields from each level of structure radiate distally. The ability of variable electric fields to radiate distally is the characteristic that is of most interest to us. In addition to having amplitude, oscillating frequency and energy like the charge at the site of the oscillating dipole, radiating electric charges have an additional characteristic of being able to be propagated to a distal site and to be detected at the site of termination.
In propagating, the electric field, depicted graphically as a wave, results from all of the constructive and destructive interferences it encounters from other sources as it propagates along its conductance pathway. The net result is that portions of some propagating waves are amplified and some portions are neutralized.
Radiating electric fields do not scatter but are modified by forces from the mix of surrounding electric fields to form discrete propagation pathways.
The distal site of propagation, in our model, is the skin.
The propagation pathway conducts both energy and bits of information.
The basis for our evaluation is to match analog wave information from the test subject with digital information in the form of pulse codes stored in the computer.
The propagation pathway is not an anatomical structure such as a nerve, but is a
non-anatomic electromagnetic channel carrying energy and information from a site of origin to a site of detection.
In the acupuncturist model energy is conducted through conductance pathways called acupuncture meridians. Our electromagnetic model detects information imbedded in the energetized conductance pathway
Our next discussion will focus on the instruments used in doing an analysis.
Reference:
Yeargers, Edward K. Basic Physics for Biology (Boca Raton: CRC Press 1992)
Vincent J, Speckhart MD, MD (H)